REFERENCES
Atzler E, Lehmann G (1931-1932): Über ein Neues Verfahren zur Darstellung der Herztätigkeit (Dielektrographie). Arbeitsphysiol. 6: 636-80.
Bache RJ, Harley A, Greenfield JC (1969): Evaluation of thoracic impedance plethysmography as an indicator of stroke volume in man. Am. J. Med. Sci. 258:(8) 100-13.
Baker LE, Hill DW, Pale TD (1974): Comparison of several pulse-pressure techniques for monitoring stroke volume. Med. Biol. Eng. 12:(1) 81-8.
Baker LE, Judy WV, Geddes LE, Langley FM, Hill DW (1971): The measurement of cardiac output by means of electric impedance. Cardiovasc. Res. Cent. Bull. 9:(4) 135-45.
Baumgartner RN, Chunlea WG, Roche AF (1988): Bioelectric impedance phase angle and body composition. Am. J. Clin. Nutr. 48: 16-23.
Cole KS, Cole RH (1941): Dispersion and absorption in dielectrics. J. Chem. Physics 9: 341-51.
Epstein BR, Foster KR (1983): Anisotropy as a dielectric property of skeletal muscle. Med. & Biol. Eng. & Comput. 21:(1) 51-5.
Geselowitz DB (1971): An application of electrocardiographic lead theory to impedance plethysmography. IEEE Trans. Biomed. Eng. BME 18:(1) 38-41.
Harley A, Greenfield JC (1968): Determination of cardiac output in man by means of impedance plethysmography. Aerospace Med. 39:(3) 248-52.
Hill DW, Lowe HJ (1973): The use of the electrical impedance technique for the monitoring of cardiac output and limb blood flow during anesthesia. Med. Biol. Eng. 11:(5) 534-45.
Hill RV, Jaensen JC, Fling JL (1967): Electrical impedance plethysmography: A critical analysis. J. Appl. Physiol. 22:(1) 161-8.
Holzer W, Polzer K, Marko A (1946): RKG. Rheography. A Method of Circulation's Investigation and Diagnosis in Circular Motion, Wilhelm Maudrich, Vienna. (English transl.)
Judy WV, Langley FM, McCowen KD, Stinnet DM, Baker LE, Johnson PC (1969): Comparative evaluation of the thoracic impedance and isotope dilution methods for measuring cardiac output. Aerospace Med. 40: 532-6.
Kinnen E, Kubicek WG, Hill DW, Turton G (1964a): Thoracic cage impedance measurements: Impedance plethysmographic determination of cardiac output (A comparative study). U.S. Air Force School of Aerospace Medicine, Brooks Air Force Base, Texas SAM-TDR-64:(15) 8.
Kinnen E, Kubicek WG, Hill DW, Turton G (1964b): Thoracic cage impedance measurements: impedance plethysmographic determination of cardiac output (An interpretative study). U.S. Air Force School of Aerospace Medicine, Brooks Air Force Base, Texas SAM-TDR-64:(23) 12.
Kinnen E, Kubicek WG, Hill DW, Turton G (1964c): Thoracic cage impedance measurements, tissue resistivity in vivo and transthoracic impedance at 100 kc. U.S. Air Force School of Aerospace Medicine, Brooks Air Force Base, Texas SAM-TDR-64:(5) 14.
Kubicek WG (1968): Minnesota Impedance Cardiograph Model 303. Instruction Manual, 4 pp. Univ. of Minnesota Press, Minneapolis.
Kubicek WG, Karnegis JN, Patterson RP, Witsoe DA, Mattson RH (1966): Development and evaluation of an impedance cardiac output system. Aerospace Med. 37:(12) 1208-12.
Kubicek WG, Patterson RP, Witsoe DA (1970): Impedance cardiography as a non-invasive method for monitoring cardiac function and other parameters of the cardiovascular system. Ann. N.Y. Acad. Sci. 170: 724-32.
Kushner RF, Shoeller DA (1986): Estimation of total body water by bioelectrical impedance analysis. Am. J. Clin. Nutr. 44:(Sept.) 417-24.
Lababidi Z, Ehmke DA, Durnin RE, Leaverton PE, Lauer RM (1970): The first derivative thoracic impedance cardiogram. Circulation 41:(4) 651-8.
Lababidi Z, Ehmke DA, Durnin RE, Leaverton PE, Lauer RM (1971): Evaluation of impedance cardiac output in children. Pediatr. 47:(5) 870-9.
Lamberts R, Visser KR, Ziljstra WG (1984): Impedance Cadiography, 160 pp. Van Gorcum, Assen, The Netherlands.
Lehr J (1972): A vector derivation useful in impedance plethysmographic field calculations. IEEE Trans. Biomed. Eng. BME-19:(2) 156-7.
Lozano A, Rosell J, Pallás-Areny R (1990): Two-frequency impedance plethysmograph: real and imaginary parts. Med. & Biol. Eng. & Comput. 28:(1) 38-42.
Lukaski HC, Johnson PE, Bolonchuk WW, Lykken GI (1985): Assessment of fat-free mass using bioelectrical impedance measurement of the human body. Am. J. Clin. Nutr. 41:(April) 810-7.
Malmivuo JA (1974): Impedance Plethysmography, Helsinki University Central Hospital, I Medical Clinic, Helsinki. (Report)
Malmivuo JA (1992): Distribution of electric current in inhomogeneous volume conductors. In Proceedings of the 8th Internat. Conference On Electrical Bio-Impedance, ed. T Lahtinen, pp. 18-20, University of Kuopio, Center for Training and Development, Kuopio, Finland.
Malmivuo JA, Orko R, Luomanmäki K (1975): Validity of impedance cardiography in measuring cardiac output in patients with atrial fibrillation. In Proceedings of The III Nordic Meeting On Medical and Biological Engineering, ed. A Uusitalo, N Saranummi, pp. 58.1-3, Finnish Society for Medical and Biological Engineering, Tampere, Finland.
Maniewski R, Katila T, Poutanen T, Siltanen P, Varpula T, Wikswo JP (1988): Magnetic measurement of cardiac mechanical activity. IEEE Trans. Biomed. Eng. 35:(9) 662-70.
Mohapatra SN (1981): Noninvasive Cardiovascular Monitoring of Electrical Impedance Technique, Pitman, London.
Mohapatra SN (1988): Impedance cardiography. In Encyclopedia of Medical Devices and Instruments, ed. JG Webster, pp. 1622-32, John Wiley & Sons, New York.
Nyboer J (1950): Plethysmography. Impedance. In Medical Physics, Vol. 2, ed. O Glasser, pp. 736-43, Year Book Pub., Chicago.
Nyboer J, Bango S, Barnett A, Halsey RH (1940): Radiocardiograms: Electrical impedance changes of the heart in relation to electrocardiograms and heart sounds. J. Clin. Invest. 19: 773. (Abstract.).
Nyboer J, Bango S, Nims LF (1943): The impedance plethysmograph and electrical volume recorder. CAM Report, OSPR : 149.
Penney BC (1986): Theory and cardiac applications of electrical impedance measurements. CRC Crit. Rev. Bioeng. 13: 227-81.
Plonsey R, Collin R (1977): Electrode guarding in electrical impedance measurements of physiological systems - A critique. Med. & Biol. Eng. & Comput. 15: 519-27.
Rosa L (1940): Diagnostische Anwendung des Kurzwellenfeldes in der Herz und Kreislaufpathologie (Radiokardiographie). Z. Kreislaufforsch. 32: 118-35.
Sakamoto K, Muto K, Kanai H, Iizuka M (1979): Problems of impedance cardiography. Med. & Biol. Eng. & Comput. 17:(6) 697-709.
Schwan HP, Kay CF (1957): Capacitive properties of body tissues. Circ. Res. 5:(4) 439-43.
Siegel JH, Fabian M, Lankau C, Levine M, Cole A, Nahmad M (1970): Clinical and experimental use of thoracic impedance plethysmography in quantifying myocardial contractility. Surgery 67: 907-17.
Tanaka K, Kanai H, Nakayama K, Ono N (1970): The impedance of blood: The effects of red cell orientation and its application. Jpn. J. Med. Eng. 8: 436-43.
Ti enko MI, Smirnov AD, Danilov LN, Aleksandrov AL (1973): Characteristics and clinical use of integral rheography. A new method of measuring the stroke volume. Kardiologiia 13: 54-62.
enko MI, Smirnov AD, Danilov LN, Aleksandrov AL (1973): Characteristics and clinical use of integral rheography. A new method of measuring the stroke volume. Kardiologiia 13: 54-62.
de Vries PMJM, Meijer JH, Vlaanderen K, Visser V, Donker AJM, Schneider H (1989): Measurement of transcellular fluid shift during haemodialysis. Med. & Biol. Eng. & Comput. 27:(March) 152-8.
van de Water JM, Dmochowski JR, Dove GB, Couch NP (1971): Evaluation of an impedance flowmeter in arterial surgery. Surgery 70:(6) 954-61.
van de Water JM, Philips PA, Thouin LG, Watanabe LS, Lappen RS (1971): Bioelectric impedance. New developments and clinical application. Arch. Surg. 102:(6) 541-7.
Wikswo JP (1975): Non-invasive magnetic measurement of the electrical and mechanical activity of the heart. Stanford University, Stanford, Thesis, pp. 304. (Ph.D. thesis)
Witsoe DA, Kottke FJ (1967): The origin of cardiogenic changes in thoracic electrical impedance (del Z). Feder. Proc. 26: 595. (Abstract No 1890).
Yamamoto Y, Yamamoto T, Öberg PÅ (1991): Impedance plethysmography in human limbs. Part 1. On electrodes and electrode geometry. Med. & Biol. Eng. & Comput. 29: 419-24.
Yamamoto Y, Yamamoto T, Öberg PÅ (1992): Impedance plethysmography for blood flow measurements in human limbs. Part 2. Influence of limb cross-sectional area. Med. & Biol. Eng. & Comput. 30:(Sept.) 518-24.
Zhao T (1992): Electrical capacitance of human blood. In Proc. Of the 8th Internat. Conf. Of Electrical Bioimpedance, 1st ed. Vol. 1, ed. T Lahtinen, pp. 185-7, University of Kuopio, Kuopio, Finland.



 enko and coworkers (1973). This method has, however, hardly been used outside the Soviet Union.
enko and coworkers (1973). This method has, however, hardly been used outside the Soviet Union.
 Determination of the cardiac stroke volume is an area in which accurate, easily applied, noninvasive methods are needed. Impedance cardiography is easy to apply, noninvasive, and also cheap; however, it has serious methodological limitations, which are discussed below. We also provide a brief overview of other applications of impedance plethysmography.
Determination of the cardiac stroke volume is an area in which accurate, easily applied, noninvasive methods are needed. Impedance cardiography is easy to apply, noninvasive, and also cheap; however, it has serious methodological limitations, which are discussed below. We also provide a brief overview of other applications of impedance plethysmography.
 The magnetic method corresponding to electric impedance plethysmography is called magnetic susceptibility plethysmography. This method may be used for monitoring blood volume changes in the thorax. Most living tissues are diamagnetic since water is their major constituent. If a strong magnetic field is applied to the region of the thorax, the movements of the heart, blood, and chest wall during the heart cycle cause variations in magnetic flux. Thus it is possible to monitor these variations with a SQUID magnetometer during the heart cycle (Wikswo, 1975; Maniewski et al., 1988). Currently, magnetic susceptibility plethysmography does not have clinical applications and, therefore, this method is not discussed in detail in this book.
The magnetic method corresponding to electric impedance plethysmography is called magnetic susceptibility plethysmography. This method may be used for monitoring blood volume changes in the thorax. Most living tissues are diamagnetic since water is their major constituent. If a strong magnetic field is applied to the region of the thorax, the movements of the heart, blood, and chest wall during the heart cycle cause variations in magnetic flux. Thus it is possible to monitor these variations with a SQUID magnetometer during the heart cycle (Wikswo, 1975; Maniewski et al., 1988). Currently, magnetic susceptibility plethysmography does not have clinical applications and, therefore, this method is not discussed in detail in this book.


 LE
LE LI
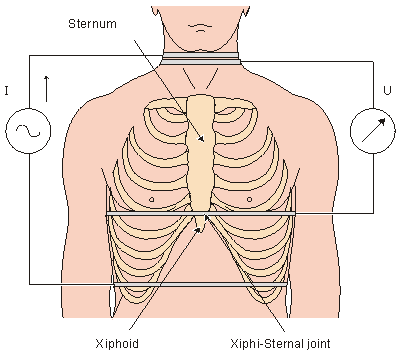
LI In Equation 25.1, the region v consists of an inhomogeneous volume conductor whose conductivity (as a function of position) at time t0 is s(t0). At t1, this has changed to s(t1), and it is this change (t1) - (t0) = Ds which is responsible for the measured impedance change DZ. Thus Equation 25.1 describes how the changes in volume conductor conductivity are converted into the impedance change evaluated from a measured voltage (at the voltage electrode pair) divided by applied current (at the current electrode pair). Note that the 4-electrode impedance method underlies Equation 25.1.
In Equation 25.1, the region v consists of an inhomogeneous volume conductor whose conductivity (as a function of position) at time t0 is s(t0). At t1, this has changed to s(t1), and it is this change (t1) - (t0) = Ds which is responsible for the measured impedance change DZ. Thus Equation 25.1 describes how the changes in volume conductor conductivity are converted into the impedance change evaluated from a measured voltage (at the voltage electrode pair) divided by applied current (at the current electrode pair). Note that the 4-electrode impedance method underlies Equation 25.1.
 A special case of Equation 25.1 is one where we consider s(t1) = es(t0), where e is very small:
A special case of Equation 25.1 is one where we consider s(t1) = es(t0), where e is very small:


 i. In these equations the corresponding variables are the measured signals: VLE and Z (= measured voltage per applied current), the distributions of sensitivity:
i. In these equations the corresponding variables are the measured signals: VLE and Z (= measured voltage per applied current), the distributions of sensitivity:  LE in both of them, as well as the source distributions:
LE in both of them, as well as the source distributions:  i and
i and  LI.
LI.
 If the introduction of the current is done with the same electrodes as the voltage measurement is made, the sensitivity distribution, that is the lead field
If the introduction of the current is done with the same electrodes as the voltage measurement is made, the sensitivity distribution, that is the lead field  LE is the same as the distribution of the applied current
LE is the same as the distribution of the applied current  LI. This technique is, however, seldom used because of the artifact due to the electrode impedance. If the current-feeding electrodes are different from those of the voltage measurement electrodes, the sensitivity distribution is the dot product of the lead fields of the voltage electrodes
LI. This technique is, however, seldom used because of the artifact due to the electrode impedance. If the current-feeding electrodes are different from those of the voltage measurement electrodes, the sensitivity distribution is the dot product of the lead fields of the voltage electrodes  LE and the current electrodes
LE and the current electrodes  LI. Thus, any previous discussion in this book on the electric and magnetic lead fields in general (Chapters 11 and 12), in the head (Chapters 13 and 14) or in the thorax (Chapters 15 ... 18 and 20) may readily be applied to impedance plethysmography. Just as in the study of electrocardiography, one can design electrode systems for impedance measurement to give special emphasis to particular regions (the aorta, the ventricles, etc.). One can even have situations where the dot product is negative in a particular region so that if the conductivity increases in that region, the impedance Z will also increase. Some examples can be found in Plonsey and Collin (1977) and Penney (1986).
LI. Thus, any previous discussion in this book on the electric and magnetic lead fields in general (Chapters 11 and 12), in the head (Chapters 13 and 14) or in the thorax (Chapters 15 ... 18 and 20) may readily be applied to impedance plethysmography. Just as in the study of electrocardiography, one can design electrode systems for impedance measurement to give special emphasis to particular regions (the aorta, the ventricles, etc.). One can even have situations where the dot product is negative in a particular region so that if the conductivity increases in that region, the impedance Z will also increase. Some examples can be found in Plonsey and Collin (1977) and Penney (1986).
 While Equation 25.1 is a suitable theoretical basis for impedance plethysmography, we are still left with considerable uncertainty how varies throughout the heart and torso or in what way the circulation modifies the thorax structure and conductivity as a function of time throughout the cardiac cycle. Further research is required to develop a physiologically adequate circulation model. Note, however, that Equation 25.1 may be more readily applied over a longer time frame (t1 - t0) to, say, the growth of a localized tumor in the thorax (other regions remaining the same).
While Equation 25.1 is a suitable theoretical basis for impedance plethysmography, we are still left with considerable uncertainty how varies throughout the heart and torso or in what way the circulation modifies the thorax structure and conductivity as a function of time throughout the cardiac cycle. Further research is required to develop a physiologically adequate circulation model. Note, however, that Equation 25.1 may be more readily applied over a longer time frame (t1 - t0) to, say, the growth of a localized tumor in the thorax (other regions remaining the same).
 In measuring bioelectric sources the reactive component of tissue impedance is not important because the frequency range is under 1 kHz. Actually, in Section 7.2.4 it was shown that it can be omitted with the assumption of quasistationarity. In impedance plethysmography (and tomography) the frequency dependence of tissue impedance is a factor which can be utilized for increasing the selectivity of the system. Because the impedance of different tissues has different reactive components, the impedance may be measured with applied currents at different frequencies (Lozano, Rosell, and Pallás-Areny, 1990). The frequencies may be selected so that the separation of certain tissues is maximized. With appropriate filtering the measurement may be done simultaneously with different frequencies in order to save measurement time.
In measuring bioelectric sources the reactive component of tissue impedance is not important because the frequency range is under 1 kHz. Actually, in Section 7.2.4 it was shown that it can be omitted with the assumption of quasistationarity. In impedance plethysmography (and tomography) the frequency dependence of tissue impedance is a factor which can be utilized for increasing the selectivity of the system. Because the impedance of different tissues has different reactive components, the impedance may be measured with applied currents at different frequencies (Lozano, Rosell, and Pallás-Areny, 1990). The frequencies may be selected so that the separation of certain tissues is maximized. With appropriate filtering the measurement may be done simultaneously with different frequencies in order to save measurement time.
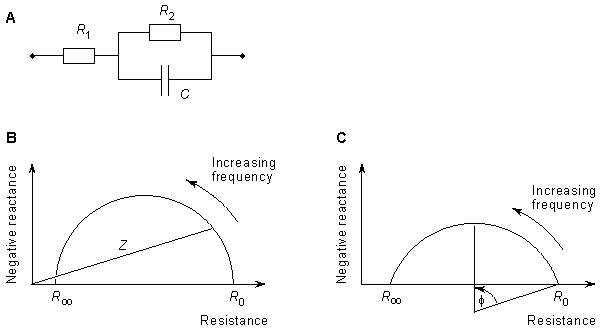
 A useful method for illustrating the behavior of tissue impedance as a function of frequency is the Cole-Cole plot (Cole and Cole, 1941). In this presentation, real component R is plotted versus imaginary component X in the complex series impedance (R + jX) with the frequency as a parameter. Figure 25.1B shows the Cole-Cole plot of a three-element impedance with a single time constant, as shown in Figure 25.1A. The Cole-Cole plot obeys the following equation:
A useful method for illustrating the behavior of tissue impedance as a function of frequency is the Cole-Cole plot (Cole and Cole, 1941). In this presentation, real component R is plotted versus imaginary component X in the complex series impedance (R + jX) with the frequency as a parameter. Figure 25.1B shows the Cole-Cole plot of a three-element impedance with a single time constant, as shown in Figure 25.1A. The Cole-Cole plot obeys the following equation:



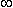
 The Cole-Cole plot is a semicircle with radius (R 0 - R
The Cole-Cole plot is a semicircle with radius (R 0 - R )/2 which intercepts the real axis at R 0 and R
)/2 which intercepts the real axis at R 0 and R , a conclusion that can be verified by noting that the real (Re) and imaginary (Im) parts of Equation 25.3 satisfy
, a conclusion that can be verified by noting that the real (Re) and imaginary (Im) parts of Equation 25.3 satisfy


 )/2 with a radius of (R 0 - R
)/2 with a radius of (R 0 - R )/2, as stated. In the three-element circuit of Figure 25.1A, R0 = R1 + R2, R
)/2, as stated. In the three-element circuit of Figure 25.1A, R0 = R1 + R2, R = R 1 , and t = R2C.
= R 1 , and t = R2C.
 In practice, the center of the semicircle is not necessarily on the real axis, but is located beneath it. The equation representing practical measurements may be described by Equation 25.4 (Schwan, 1957):
In practice, the center of the semicircle is not necessarily on the real axis, but is located beneath it. The equation representing practical measurements may be described by Equation 25.4 (Schwan, 1957):


 The reactive component of human blood has been studied, for example, by Tanaka et al. (1970) and Zhao (1992). The reactive component of tissue impedance seems to have an important role in impedance plethysmography, as will be discussed later in this Chapter in connection with determining body composition..
The reactive component of human blood has been studied, for example, by Tanaka et al. (1970) and Zhao (1992). The reactive component of tissue impedance seems to have an important role in impedance plethysmography, as will be discussed later in this Chapter in connection with determining body composition..



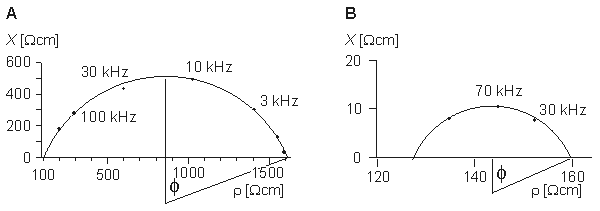
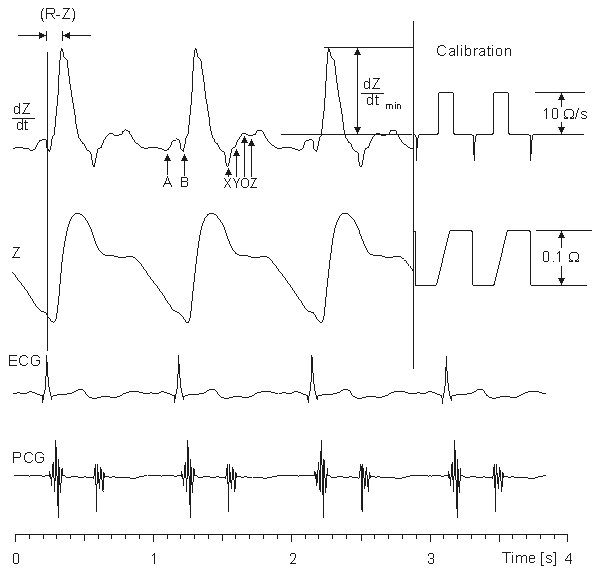









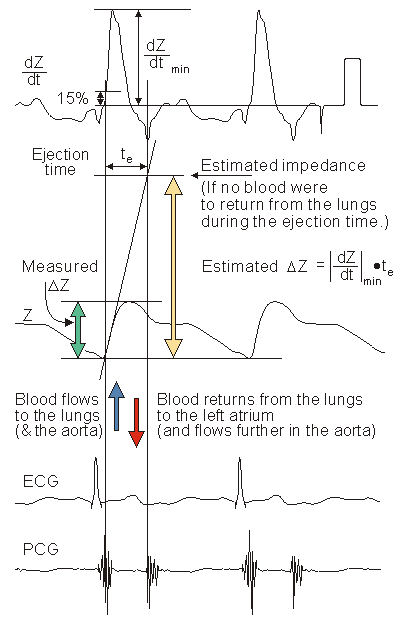

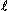 /min before and 9.5
/min before and 9.5