Изображение траектории движения ЛА представляется в виде его положения в фазовых
координатах, например как на Рис.1 Н - М, где М - число Маха.
На изменение "фазовых" координат ЛА накладываются некоторые ограничения
ХОGХ. Вектор U - "свободный"
вектор-функция (в том смысле, что он находится в распоряжении лица, выбирающего
управляющую функцию. Однако выбор величины U обычно стеснен какими-либо
ограничениями UОGU. В соответствии с общей
задачей наведения необходимо за время Т перевести ЛА из состояния
Х(0)=Х0 в состояние Х(Т)=ХТ путем выбора подходящего U.
Следовательно, принципиально можно достичь цели, удовлетворив всем ограничениям.
Функция U(Х) после того, как она выбрана, является формализованным описанием
достижения цели. Эта цель может быть формализирована в терминах минимума
некоторого функционала вида:
Обычно в практических целях необходимо получить
максимальную (max) или наибольшую (
Sup) выгоду, т.е. расходы должны быть
минимальными
Ji(U) → inf, при i=0
ёN-1. Вид заданной пространственно-временной
траектории зависит от типа летательного аппарата, целей полета и определяется
путей минимизации уровня обобщенных затрат, например расхода топлива
Gт
и времени полета
tп, по соотношению -
min
J = min [λ•Gт + (1-λ)•tп],
где - множитель, характеризующий относительную ценность составляющих.
При λ = 0 пространственно-временная траектория соответствует
минимальному времени выполнения навигационно-тактических задач, а при λ = 1
- минимальному расходу топлива. При полете с постоянной тягой
Р расход
топлива за время
t составит:
Gт = -Ср•P•t , где Сp - секундный расход,
является одной из основных характеристик двигателя.
Выбор оптимальной траектории относится к классу задач на условный экстремум и
может быть осуществлен, например, методом динамического программирования. Базой
для решения этой задачи является система нелинейных дифференциальных уравнений,
описывающих движение летательного аппарата (Раздел "ЗАДАНИЕ").
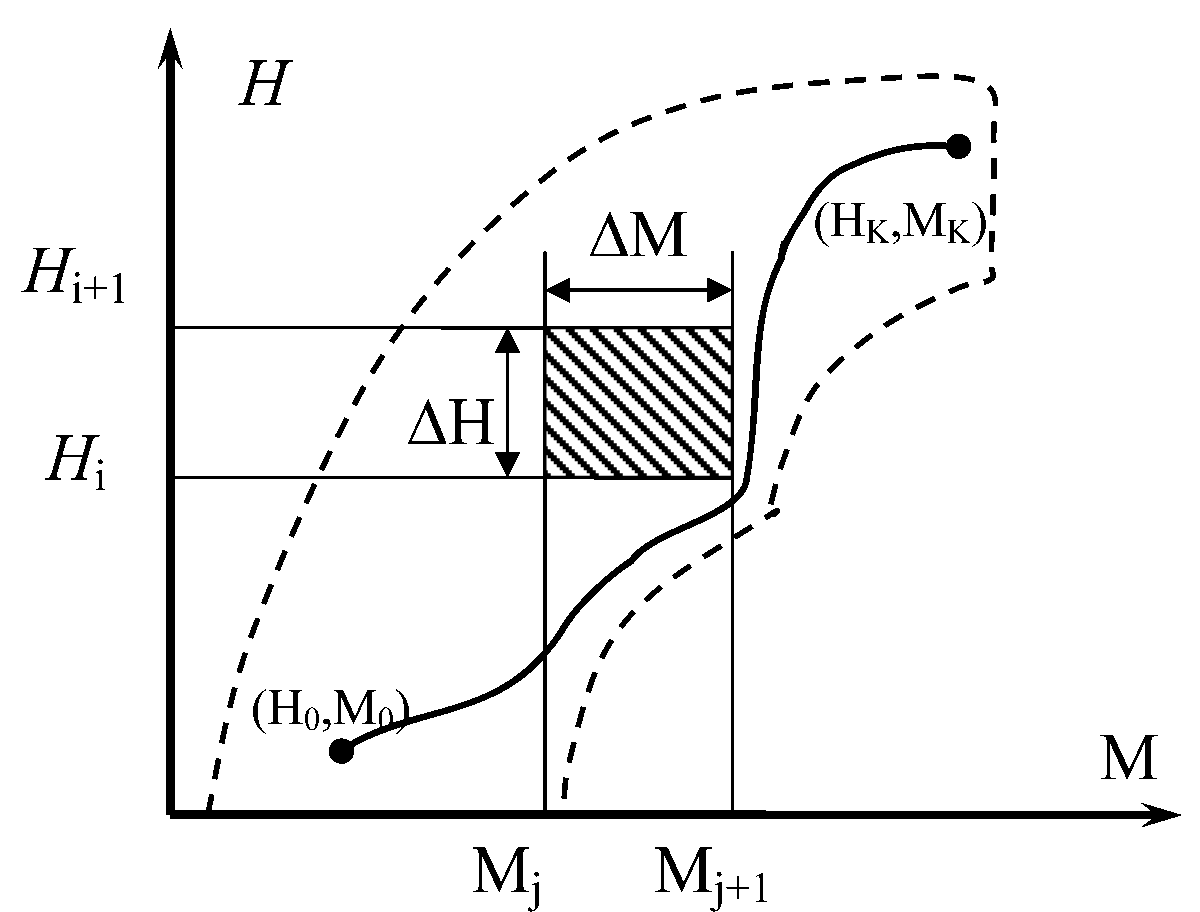
Рис.1. Примерная область допустимых режимов полета ЛА.
Процесс оптимизации в виде последовательности отдельных
этапов (шагов).
Основу этого метода составляет принцип оптимальности, утверждающий, что каков бы
ни был путь достижения некоторого состояния системы, последующие решения должны
принадлежать оптимальной программе для оставшейся части пути, начинающейся с
этого состояния. Применение сформулированного принципа позволяет получить все
используемые в динамическом программировании функциональные рекуррентные
соотношения.
Пусть система описывается с помощью рекуррентных уравнений:
Х(k+1) = f k+1[Х(k), U(k)] ,
где k = 0, 1, ... N-1 , X(0) задано.
Целью управления является минимизация функционала
J =
т
Т L(
X, U)dt =
ΣN-1
L[Х(i), U(i)] , где i = 0, 1, ... N-1.
Естественно, что минимальное значение функционала
J зависит от начального
состояния X(0) (которое неуправляемо). Обозначим этот минимум через
j
N[X(0)]. Нетрудно видеть, что справедливы следующие соотношения:
jN[X(0)] =
minU(0)minU(1)...minU(N-1)
{L[X(0), U(0)]+L[X(l), U(l)]+ ... +L[X(N-1), U(N-1)]}=
= minU(0){L[X(0), U(0)] } + minU(1)...minU(N-1)
{L[X(l), U(l)]+...+L[X(N-1), U(N-1)] } =
= minU(0){L[X(0), U(0)] } + jN-1[X(1)] .
Здесь
jN-1[X(1)] можно трактовать как минимальное значение
критерия качества для процесса длительностью в N-1 шагов и имеющего начальное
состояние X(1). Аналогично получается следующее соотношение:
jN-1[X(1)] =
minU(1){L[X(1), U(1)] } + jN-2[X(2)] ,
а также обобщение для процесса управления с N-q шагами, имеющего в качестве
начального состояния X(q-1):
jN-q[X(1)] =
minU(q){L[X(q), U(q)] } + jN-q[X(q)] ,
где 1 =< q =< N-1.
Последнее соотношение является дискретным вариантом уравнения Беллмана.
Практический расчет траектории.
На практике фазовое пространство полетной области зачастую задается в
координатах Н - М. Шаг разбиения полетной области (см. Рис.1.) на элементарные
подобласти для задач данного класса равен:
ΔН = 1000м, ΔМ = 0,25 при первых, отладочных
расчетах;
ΔН = 250…500м, ΔМ = 0,05 при более точном построении
параметрической траектории.
В соответствии с этим количество элементарных подобластей:
n = mхh,
где m = (Mmax - Mmin)/ΔM ,
h = (Hmax - Hmin)/ΔH.
При дальнейшем расчете есть смысл перейти от М =
V/a к
V, где
а - скорость звука в воздухе на данной высоте полета.
Н и
V выбирается с таким расчетом, чтобы в пределах элементарной подобласти
параметры стандартной атмосферы, аэродинамические характеристики летательного
аппарата, тяга двигателей и т.д. менялись незначительно или описывались
простыми зависимостями. Внутри каждой элементарной подобласти, ограниченной
точками с координатами
Нi,
Нi+1,
Vi,
Vi+1 допускается движение по трем
элементарным траекториям, соответствующим:
- режиму "разгон" летательного аппарата при постоянной высоте полета -
(элементарная траектория A-F , Рис.2.), при разгоне летательного аппарата на
постоянной высоте d
Н/dt = 0 и Θ = 0;
- режиму "подъем" летательного аппарата с постоянным числом М полета -
(элементарная траектория В-F, Рис.2.), при наборе высоты летательным аппаратом с
постоянной скоростью d
V/dt = 0 и d
V/d
Н = 0;
- режиму "подъем-разгон" летательного аппарата с постоянным углом наклона
траектории dΘ/dt = 0 - (элементарная траектория С-F , Рис.2.), примем
допущение о линейном изменении скорости по высоте полета на каждой элементарной
траектории: d
H/d
V = K = const .
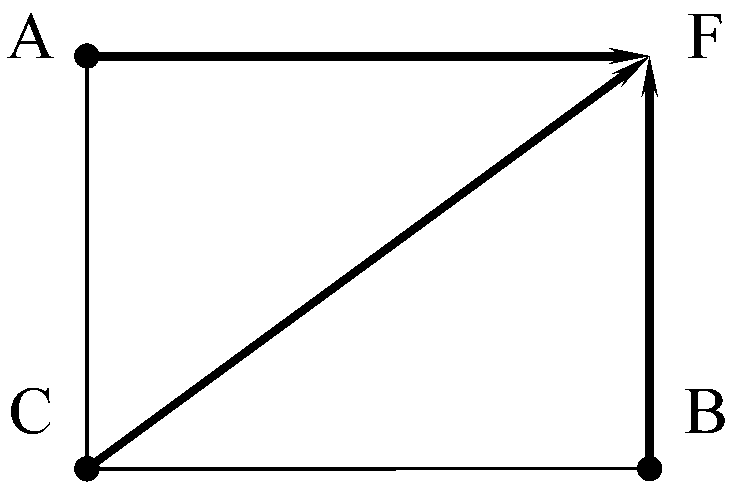
Рис.2. Элементарная подобласть.
Фазовая траектория, переводящая точку S, изображающую летательный аппарат на
фазовой плоскости (
V,
Н), из положения So = (
Vo,
Нo)
в положение Sк = (
Vк,
Нк), в данном случае являются некоторой
ломаной, состоящей из отрезков элементарных траекторий "разгон", "подъем" и
"подъем-разгон". Тогда весь процесс набора высоты и скорости будет состоять из
n =< m + h шагов.
Точка S из So в Sк может перемещаться по горизонтальным и вертикальным и по
наклонным отрезкам. Запишем на каждом из этих отрезков соответствующий расход
горючего (затрата времени). Каждой траектории, переводящей точку S из Sо в Sк,
соответствует свой расход горючего (или время полета)
J.
Расчеты построены таким образом, чтобы при рассмотрении некоторой точки F (узла
решетки разбиения) с координатами
HF и
VF
рассчитывались значения функции веса согласно виду выбранного функционала
J для элементарных траекторий трех видов, приходящих в эту точку из точек
А, В, С. Координаты точек выхода элементарных траекторий будут иметь значения:
А(HF , VF - ΔV),
В(HF - ΔН, VF),
С(HF - ΔН , VF
- ΔV) (Рис. 2).
При выборе траектории движения величина функционала
J вычисляется как
сумма значений функции веса на всех элементарных траекториях, по которым
движется самолет из заданной начальной точки в конечную. Для примера возьмем
полетную область 4
х4 узла,
(частный случай позволит проследить процесс оптимизации целиком от начала до
конца). Займемся оптимизацией последнего шага. Рассмотрим правый верхний угол
прямоугольной сетки на плоскости (
V, Н) (Рис.3.) с отмеченными значениями
расхода горючего (или времени полета), необходимого для достижения
соответствующего состояния (Рис.4.). В конце предпоследнего (шага с номером
n-1) точка S может оказаться либо в точке S
4-3 (первый индекс
обозначает нумерацию по скорости, второй - нумерацию по высоте возможного
состояния, причем нумерация ведется по диагонали снизу вверх), либо в точке
S
3-4, либо для режима подъем-разгон S
3-3, из которых за
один последний шаг можно перейти в точку Sк единственным образом. Около каждой
из этих точек запишем минимальные (и в данном случае неизбежные) расходы
(горючего или времени), которые необходимо потратить, чтобы из них попасть в
точку Sк. Стрелкой обозначим направление движения точки S из данного состояния.
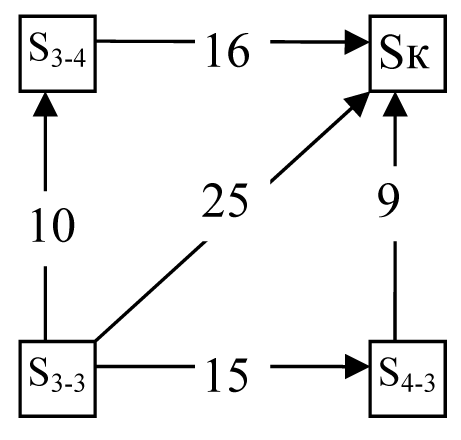
Рис.3. Правый угол на сетке
V - H .
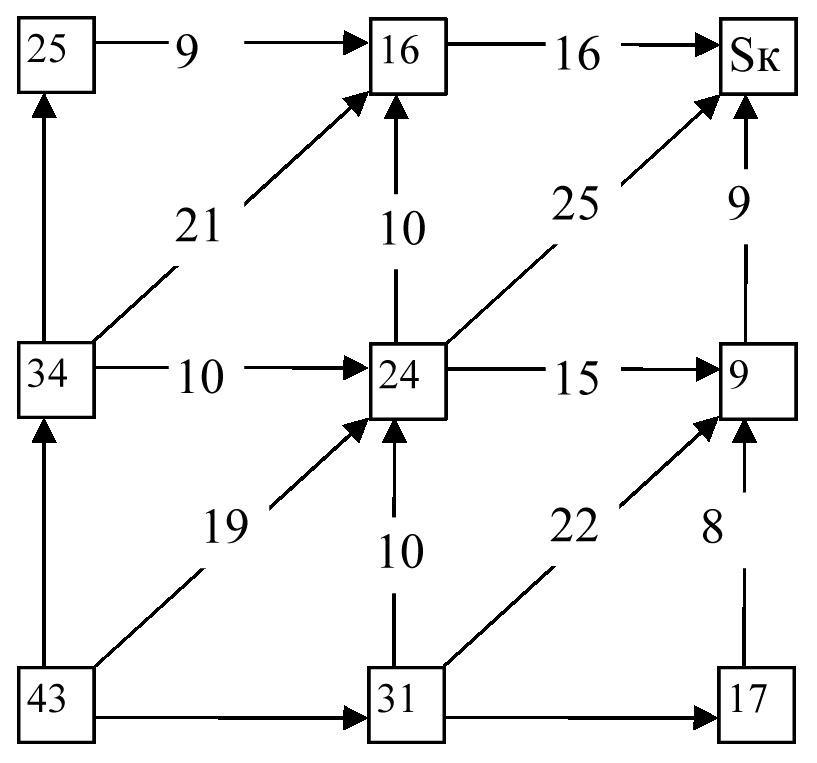
Рис.4. Исходы предпоследнего шага.
Перейдем к выбору оптимального управления на предпоследнем шаге. Для этого
рассмотрим все исходы предыдущего для него (предпредпоследнего) шага, из
которого за два шага можно попасть в точку Sк. Таких исходов 4 - точки
S
3-3, S
2-2, S
2-4, S
4-2, (Pис. 4 и 3).
Переход из точек S
2-2, S
2-4, S
4-2 в точку Sк за
два шага можно выполнить лишь единственным образом со стоимостью в 17 и 25
единиц горючего (времени). Оптимальное движение из этих точек, как уже
указывалось, отмечено стрелками. Из точки S
3-3 в точку Sк за два
шага можно попасть двумя способами и одним способом за один шаг. В первом случае
потребуется 15 + 9 = 24 единицы , во втором 10 + 16 = 26 единиц и в третьем 25,
хотя и за один шаг. Наименьший расход горючего (времени) будет при перемещении
направо вверх (его отмечаем жирной стрелкой). Отметим на схеме оптимальный
расход горючего(времени) в узле, требуемый для перехода из данного состояния в
конечное. Если оптимальных управлений несколько, то возьмем произвольное из них.
Далее аналогично оптимизируем следующий, рассматривая все точки, из которых
перейти в точку Sк.
Исходя из количества элементарных подобластей, элементарных траекторий "разгон"
будет (m+1)
хh, элементарных
траекторий "подъем" будет
m
х(h+1), а элементарных
траекторий "подъем-разгон" будет
m
хh . При составлении программы
расчета есть смысл, значения весовых функций для элементарных траекторий,
присваивать соответствующему элементу одной из матриц А - "разгон", В - "подъем"
и С - "подъем-разгон", согласно нумерации узла. При практическом расчете методом
динамического программирования для каждого узла
HF и
VF важной информацией является суммарное минимальное значение
функции веса и направление движения до следующего узла. Эта информация может
быть по мере расчета от конечной точки
Hmax и
Vmax присваиваться
элементам двух матриц размером
(m+1)
х(h+1), по количеству
узлов. Они и будут полностью характеризовать и определять оптимальную траекторию
движения летательного аппарата.



