In Chapter 12 it was pointed out that the origin of the biomagnetic field is the electric activity of biological tissue. This bioelectric activity produces an electric current in the volume conductor which induces the biomagnetic field. This correlation between the bioelectric and biomagnetic phenomena is, of course, not limited to the generation of the bioelectric and biomagnetic fields by the same bioelectric sources. This correlation also arises in the stimulation of biological tissue.
 Magnetic stimulation is a method for stimulating excitable tissue with an electric current induced by an external time-varying magnetic field. It is important to note here that, as in the electric and magnetic detection of the bioelectric activity of excitable tissues, both the electric and the magnetic stimulation methods excite the membrane with electric current. The former does that directly, but the latter does it with the electric current which is induced within the volume conductor by the time-varying applied magnetic field.
Magnetic stimulation is a method for stimulating excitable tissue with an electric current induced by an external time-varying magnetic field. It is important to note here that, as in the electric and magnetic detection of the bioelectric activity of excitable tissues, both the electric and the magnetic stimulation methods excite the membrane with electric current. The former does that directly, but the latter does it with the electric current which is induced within the volume conductor by the time-varying applied magnetic field.
 The reason for using a time-varying magnetic field to induce the stimulating current is, on the one hand, the different distribution of stimulating current and, on the other hand, the fact that the magnetic field penetrates unattenuated through such regions as the electrically insulating skull. This makes it possible to avoid a high density of stimulating current at the scalp in stimulating the central nervous system and thus avoid pain sensation. Also, no physical contact of the stimulating coil and the target tissue is required, unlike with electric stimulation.
The reason for using a time-varying magnetic field to induce the stimulating current is, on the one hand, the different distribution of stimulating current and, on the other hand, the fact that the magnetic field penetrates unattenuated through such regions as the electrically insulating skull. This makes it possible to avoid a high density of stimulating current at the scalp in stimulating the central nervous system and thus avoid pain sensation. Also, no physical contact of the stimulating coil and the target tissue is required, unlike with electric stimulation.
 The first documents on magnetic stimulation described the stimulation of the retina by Jacques d'Arsonval (1896) and Silvanus P. Thompson (1910). The retina is known to be very sensitive to stimulation by induced currents, and field strengths as low as 10 mT rms at 20 Hz will cause a stimulation (Lövsund, Öberg, and Nilsson, 1980).
The first documents on magnetic stimulation described the stimulation of the retina by Jacques d'Arsonval (1896) and Silvanus P. Thompson (1910). The retina is known to be very sensitive to stimulation by induced currents, and field strengths as low as 10 mT rms at 20 Hz will cause a stimulation (Lövsund, Öberg, and Nilsson, 1980).
 From the pioneering works of d'Arsonval and Thompson it took some time before the magnetic method was applied to neuromuscular stimulation. Bickford and Fremming (1965) used a damped 500 Hz sinusoidal magnetic field and demonstrated muscular stimulation in animals and humans. Magnetic stimulation of nerve tissue was also demonstrated by Öberg (1973). The first successful magnetic stimulation of superficial nerves was reported by Polson et al. in 1982 (Polson, Barker, and Freeston, 1982).
From the pioneering works of d'Arsonval and Thompson it took some time before the magnetic method was applied to neuromuscular stimulation. Bickford and Fremming (1965) used a damped 500 Hz sinusoidal magnetic field and demonstrated muscular stimulation in animals and humans. Magnetic stimulation of nerve tissue was also demonstrated by Öberg (1973). The first successful magnetic stimulation of superficial nerves was reported by Polson et al. in 1982 (Polson, Barker, and Freeston, 1982).
 Transcranial stimulation of the motor cortex is the most interesting application of magnetic stimulation because the magnetic field (unlike the electric current) penetrates through the skull without attenuation. The first transcranial stimulation of the central nervous system was achieved in 1985 (Barker and Freeston, 1985; Barker, Freeston, Jalinous, Merton, and Morton, 1985; Barker, Jalinous, and Freeston, 1985). A more complete history of magnetic stimulation may be found from a review article of Geddes (1991).
Transcranial stimulation of the motor cortex is the most interesting application of magnetic stimulation because the magnetic field (unlike the electric current) penetrates through the skull without attenuation. The first transcranial stimulation of the central nervous system was achieved in 1985 (Barker and Freeston, 1985; Barker, Freeston, Jalinous, Merton, and Morton, 1985; Barker, Jalinous, and Freeston, 1985). A more complete history of magnetic stimulation may be found from a review article of Geddes (1991).
  | (22.1) |
| where | 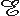 | = electromotive force (emf) [V] |
| F | = magnetic flux [Wb = Vs] | |
| t | = time [s] |
Corresponding to a magnetic field 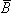 the flux
the flux 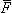 , linking the circuit is given by
, linking the circuit is given by  , where the integral is taken over any surface whose periphery is the circuit loop.
, where the integral is taken over any surface whose periphery is the circuit loop.
 If the flux is due to a coil's own current I, the flux is defined as: F = LI, where L is the inductance of the coil and the emf can be written
If the flux is due to a coil's own current I, the flux is defined as: F = LI, where L is the inductance of the coil and the emf can be written
  | (22.2) |
| where | L | = inductance of the coil [H =Wb/A = Vs/A] |
| I | = current in the coil [A] |
and other variables are as in Equation 22.1.
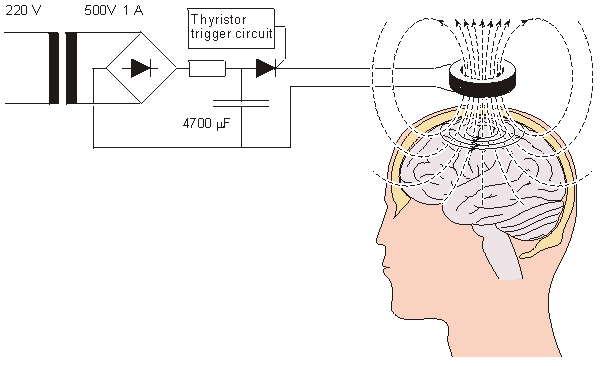
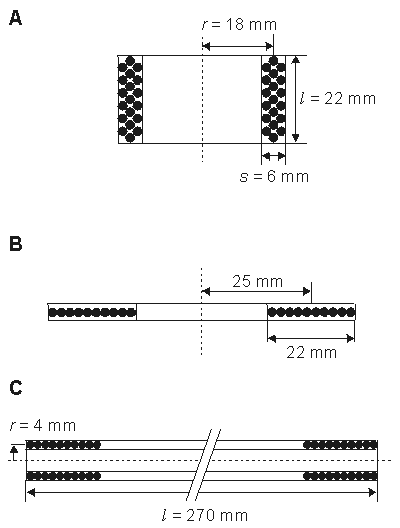
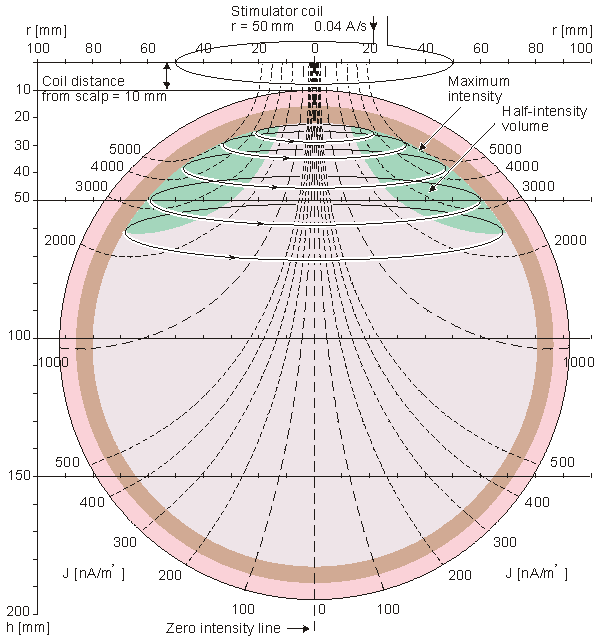
 The magnitude of induced emf is proportional to the rate of change of current, dI/dt. The coefficient of proportionality is the inductance L. The term dI/dt depends on the speed with which the capacitors are discharged; the latter is increased by use of a fast solid-state switch (i.e., fast thyristor) and minimal wiring length. Inductance L is determined by the geometry and constitutive property of the medium. The principal factors for the coil system are the shape of the coil, the number of turns on the coil, and the permeability of the core. For typical coils used in physiological magnetic stimulation, the inductance may be calculated from the following equations:
The magnitude of induced emf is proportional to the rate of change of current, dI/dt. The coefficient of proportionality is the inductance L. The term dI/dt depends on the speed with which the capacitors are discharged; the latter is increased by use of a fast solid-state switch (i.e., fast thyristor) and minimal wiring length. Inductance L is determined by the geometry and constitutive property of the medium. The principal factors for the coil system are the shape of the coil, the number of turns on the coil, and the permeability of the core. For typical coils used in physiological magnetic stimulation, the inductance may be calculated from the following equations:









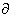 Ex /
Ex /