In this chapter, we develop expressions for electric sources of bioelectric origin. These sources are generated by the passage of current across the membrane of active (excitable) cells, which may be either nerve or muscle. We consider excitable tissue with very simple models - mainly single cylindrical fibers. But the results are useful in later chapters when considering whole organs which can be thought of as composed of many such elements. We see that bioelectric sources can be described as surface/volume distributions of two types of source element, namely the monopole and/or dipole. Because of the fundamental importance of the monopole and dipole source, we first proceed to a description of the fields generated by each.
8.2 SOURCE MODELS
8.2.1 Monopole
PRECONDITIONS:
The simplest source configuration is the point source or monopole. If we consider a point current source of magnitude I0 lying in a uniform conducting medium of infinite extent and conductivity s, then current flow lines must be uniform and directed radially. As a consequence, for a concentric spherical surface of arbitrary radius r, the current density J crossing this surface must be uniform and will equal I0 divided by the total surface area. That is
since the total current is conserved. Because the current is everywhere in the radial direction, the current density expressed as a vector is
where
From Ohm's law it follows that
Applying Equations 8.3 and 8.4 to 8.2 results in
To satisfy Equation 8.5, only the component of
and integration with respect to r leaves us with
As suspected above, F is a constant on surfaces where r is constant (i.e., concentric spheres). Normally the potential for r
where each monopole is located at (x, y, z) while the field point is at (x', y', z').
PRECONDITIONS:
In bioelectricity one can never have a single isolated monopole current source because of the need to conserve charge. But collections of positive and negative monopole sources are physically realizable if the total sum is zero. The simplest collection, and one that reflects a fundamental bioelectric source, is the dipole. The dipole consists of two monopoles of opposite sign but equal strength I0 (often termed source and sink) separated by a very small distance, d. In fact, the strict definition requires d
where
The directional derivative in Equation 8.10 equals the component of the gradient in the direction
and, finally since I0d = p
The accuracy of Equation 8.10 improves as d
where
and
In Equation 8.15 the angle q is the polar (colatitude) angle. The above expressions can be confirmed by noting that the gradient operator (in Equation 8.13) acts on the source (unprimed) coordinates in Equation 8.8.
8.2.3 Single Isolated Fiber: Transmembrane Current Source
PRECONDITIONS:
Figure 8.2 illustrates a long, thin excitable fiber lying in a uniform conducting medium of conductivity so and of unlimited extent. If we assume the existence of a propagating nerve impulse, then the activation currents are associated with a transmembrane current distribution im(x). Since the fiber is very thin and there is axial symmetry, we can describe the transmembrane current as a function of the axial variable x only. Thus the source description is one-dimensional. The dimension of im(x) is current per unit length. A small element of current im(x)dx can, therefore, be considered to behave like a point current source (a monopole) within the extracellular medium. Consequently, from Equation 8.7, we have
where r is given by Equation 8.8, Fo is the potential field and so is the conductivity outside the fiber (i.e.,extracellular conductivity). Integration over the fiber (i.e., with respect to x) gives the total field as
where the source is assumed to lie on the fiber axis, at (x, 0, 0), and the (fixed) field point is at (x', y', z').
so that Equation 8.17 may be written
Source: Monopole in a fixed location
Conductor: Infinite, homogeneous

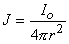
(08.01)

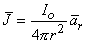
(08.02)  r = unit vector in the radial direction, where the origin is at the point source.
r = unit vector in the radial direction, where the origin is at the point source.
 Associated with the current flow field defined by Equation 8.2 is a scalar potential field F. Since the field is everywhere radial, there should be no variation of potential along a transverse direction, namely that on which r is a constant. Consequently, we expect isopotential surfaces to be a series of concentric spheres surrounding the point source with diminishing potentials for increasing values of r. In a formal sense, it is known from field theory that the electric field
Associated with the current flow field defined by Equation 8.2 is a scalar potential field F. Since the field is everywhere radial, there should be no variation of potential along a transverse direction, namely that on which r is a constant. Consequently, we expect isopotential surfaces to be a series of concentric spheres surrounding the point source with diminishing potentials for increasing values of r. In a formal sense, it is known from field theory that the electric field  is related to a scalar potential F by
is related to a scalar potential F by

 = -
= -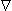 F
F(08.03)

 = s
= s
(08.04)

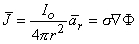
(08.05) 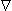 F in the direction of r can arise. This leads to
F in the direction of r can arise. This leads to

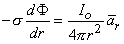
(08.06)

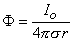
(08.07) 
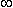 is set to zero, which accounts for having chosen the constant of integration in Equation 8.7 equal to zero. We note from Equation 8.7 that equipotential surfaces are indeed concentric spheres and that the potential magnitude is inversely proportional to the radius (with the origin at the monopole source).
is set to zero, which accounts for having chosen the constant of integration in Equation 8.7 equal to zero. We note from Equation 8.7 that equipotential surfaces are indeed concentric spheres and that the potential magnitude is inversely proportional to the radius (with the origin at the monopole source).
 It is not always convenient to place the coordinate system origin at the point source (e.g., when considering several such sources). In this case it is desirable to distinguish the coordinates of the point source(s) from that of the field point, and we do this by using primes for the field point coordinates. Equation 8.7 then applies with, r given by
It is not always convenient to place the coordinate system origin at the point source (e.g., when considering several such sources). In this case it is desirable to distinguish the coordinates of the point source(s) from that of the field point, and we do this by using primes for the field point coordinates. Equation 8.7 then applies with, r given by

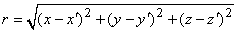
(08.08)  The field described by Equation 8.7 for a point current source is identical to the electrostatic field from a point charge, provided that I0 is replaced by Q0 (the charge magnitude), s is replaced by e (the permittivity), and
The field described by Equation 8.7 for a point current source is identical to the electrostatic field from a point charge, provided that I0 is replaced by Q0 (the charge magnitude), s is replaced by e (the permittivity), and  replaced by
replaced by  . This result is not surprising since if the aforementioned exchanges are made, the governing equations for current flow convert exactly into those for electrostatics. This means that simply by interchanging symbols, solutions to problems in electrostatics can be converted into solutions to equivalent problems in current flow (and vice versa).
. This result is not surprising since if the aforementioned exchanges are made, the governing equations for current flow convert exactly into those for electrostatics. This means that simply by interchanging symbols, solutions to problems in electrostatics can be converted into solutions to equivalent problems in current flow (and vice versa).
 The aforementioned is an example of duality. It can be a useful tool when there is an extensive literature already in existence. Sometimes there may be a limitation in physically realizing a condition in one or the other dual systems. For example, one can have zero conductivity, but the permittivity can never be less than that of vacuum. Also, while one can have a point charge, one cannot actually have a physical point source.
The aforementioned is an example of duality. It can be a useful tool when there is an extensive literature already in existence. Sometimes there may be a limitation in physically realizing a condition in one or the other dual systems. For example, one can have zero conductivity, but the permittivity can never be less than that of vacuum. Also, while one can have a point charge, one cannot actually have a physical point source.
 The reader may wonder why there is an interest in a point current source when such is not physically obtainable. One reason is that in a limited region, the fields may behave as if they arise from such a source (we say that the source is equivalent). Second, one can actually have two point sources of opposite polarity, in which case the field of interest can be found by the superposition of point source fields. In fact, this very situation is examined in the next section..8.2.2 Dipole
The reader may wonder why there is an interest in a point current source when such is not physically obtainable. One reason is that in a limited region, the fields may behave as if they arise from such a source (we say that the source is equivalent). Second, one can actually have two point sources of opposite polarity, in which case the field of interest can be found by the superposition of point source fields. In fact, this very situation is examined in the next section..8.2.2 Dipole
Source: Dipole in a fixed location
Conductor: Infinite, homogeneous
 0, I0
0, I0 
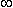 with p = I0d remaining finite in the limit. The quantity p is the dipole moment or dipole magnitude. The dipole is a vector whose direction is defined from the negative point source to the positive. In fact, if
with p = I0d remaining finite in the limit. The quantity p is the dipole moment or dipole magnitude. The dipole is a vector whose direction is defined from the negative point source to the positive. In fact, if  is the displacement from negative to positive point source and
is the displacement from negative to positive point source and  d a unit vector in that direction, then
d a unit vector in that direction, then

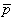 = Io
= Io = Io d
= Io d d
d (08.09) 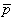 = the dipole vector.
= the dipole vector.
 A dipole of arbitrary orientation is illustrated in Figure 8.1, where the coordinate system origin is placed at the negative pole. If the positive pole were also at the origin, the sources would cancel each other and their field would be zero. Consequently, the field arising from the displacement of the positive pole from the origin to its actual position (shown in Figure 8.1) is, in fact, the dipole field. But this can be found by examining the expression describing the potential of the positive monopole and evaluating the change in potential brought about by moving the monopole from the origin to its dipole position. And this, in turn, can be approximated from the first derivative of the monopole's potential field with respect to the source coordinates evaluated at the origin (as in a Taylor series representation). Specifically, to obtain the dipole field, a derivative of F (as given in Equation 8.7) is taken with respect to the direction
A dipole of arbitrary orientation is illustrated in Figure 8.1, where the coordinate system origin is placed at the negative pole. If the positive pole were also at the origin, the sources would cancel each other and their field would be zero. Consequently, the field arising from the displacement of the positive pole from the origin to its actual position (shown in Figure 8.1) is, in fact, the dipole field. But this can be found by examining the expression describing the potential of the positive monopole and evaluating the change in potential brought about by moving the monopole from the origin to its dipole position. And this, in turn, can be approximated from the first derivative of the monopole's potential field with respect to the source coordinates evaluated at the origin (as in a Taylor series representation). Specifically, to obtain the dipole field, a derivative of F (as given in Equation 8.7) is taken with respect to the direction  (a directional derivative) and then multiplied by the magnitude of d. Thus, denoting the dipole field Fd, and based on Equation 8.7, we have
(a directional derivative) and then multiplied by the magnitude of d. Thus, denoting the dipole field Fd, and based on Equation 8.7, we have

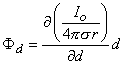
(08.10) 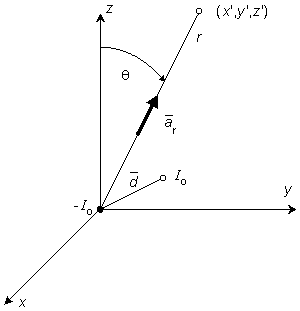
Figure 8.1. Dipole consisting of a sink -I0 at origin and a source I0 at radius vector
 , where d
, where d  0. Also illustrated is a field point at radius vector r
0. Also illustrated is a field point at radius vector r r and polar (colatitude) angle q.
r and polar (colatitude) angle q. so that
so that

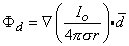
(08.11)

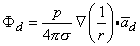
(08.12)  0, and in fact, p (as noted earlier) is normally defined in the limit that d
0, and in fact, p (as noted earlier) is normally defined in the limit that d  0, I
0, I 
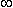 , such that the product I0d is finite and is equal to p. Consequently, Equation 8.12 is a rigorous (exact) expression for a mathematically defined dipole.
, such that the product I0d is finite and is equal to p. Consequently, Equation 8.12 is a rigorous (exact) expression for a mathematically defined dipole.
 If the coordinate axes are oriented so that the dipole is directed along z- (the polar) axis and the dipole is placed at the origin, then carrying out the gradient operation in Equation 8.12 and noting that
If the coordinate axes are oriented so that the dipole is directed along z- (the polar) axis and the dipole is placed at the origin, then carrying out the gradient operation in Equation 8.12 and noting that

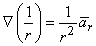
(08.13)  r is oriented from the source point to field point, we obtain for the field of a dipole
r is oriented from the source point to field point, we obtain for the field of a dipole

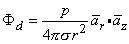
(08.14)

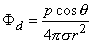
(08.15)  A comparison of the dipole field to a monopole field, by contrasting Equation 8.15 with Equation 8.7, shows that the dipole field varies as (1/r)2 whereas the monopole field varies as (1/r). In addition, the dipole equipotential surfaces are not concentric spheres but, rather, are more complicated, because of the factor cosq. The maximum dipole potential, for a given value of r, is on the polar axis (z axis).
A comparison of the dipole field to a monopole field, by contrasting Equation 8.15 with Equation 8.7, shows that the dipole field varies as (1/r)2 whereas the monopole field varies as (1/r). In addition, the dipole equipotential surfaces are not concentric spheres but, rather, are more complicated, because of the factor cosq. The maximum dipole potential, for a given value of r, is on the polar axis (z axis).
Source: Active fiber of finite or infinite length with circular cross-section
Conductor: Infinite, homogeneous

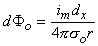
(08.16)

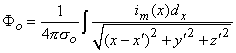
(08.17)  We may apply the equations derived in Chapter 3, Section 3.4.2, to the fiber in Figure 8.2. We may approximate that the resistance of the interstitial medium ro
We may apply the equations derived in Chapter 3, Section 3.4.2, to the fiber in Figure 8.2. We may approximate that the resistance of the interstitial medium ro  0 and that similarly the potential in the interstitial medium Fo
0 and that similarly the potential in the interstitial medium Fo  0. Using these approximations and Equation 3.42 and noting that Fi - Fo
0. Using these approximations and Equation 3.42 and noting that Fi - Fo 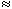 Vm we obtain
Vm we obtain

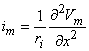
(08.18) 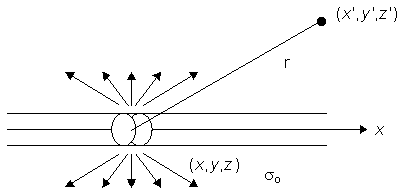
Figure 8.2. A long thin fiber is shown embedded in a uniform conducting medium of conductivity so and infinite in extent. The transmembrane current density is described by im(x) so that im(x)dx, illustrated, behaves as a point source in the extracellular medium.
 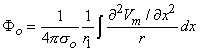 | (08.19) |
In Equation 8.19, r is given by
 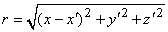 | (08.20) |
Using the cylindrical resistance formula for ri = 1/(pa2si) based on a conductivity si inside the cell, converts Equation 8.19 into
where a = the fiber radius.
and then recalculating Fo. This will produce an improved Fo. In fact, this iterative procedure can be repeated until a desired degree of convergence results. Such a procedure is followed in Henriquez and Plonsey (1988), and is seen to converge very rapidly, demonstrating that for typical physiological situations the first-order approximation (given by Equation 8.21) is entirely satisfactory.
or
where
8.2.4 Discussion of Transmembrane Current Source
The expression in Equation 8.17 describes the field in the extracellular volume arising from transmembrane current elements. It is therefore limited to the evaluation of potentials outside the cell and is not valid for describing intracellular fields.
The source identified by Equation 8.28 is a double layer lying on the membrane surface, whose strength is (soFo - siFi)dS and whose orientation is along the outward surface normal (Plonsey, 1974). The field point P in Equation 8.28 can be intracellular as well as extracellular; however, the coefficient P takes on the conductivity at the field point.
8.4.2 Field of an Isolated Cylindrical Fiber
PRECONDITIONS:
where the integration proceeds over the cross-sectional area A, as well as axially. If the field point is at a large distance compared to the radius, then Equation 8.29 reduces to Equation 8.21 and Equation 8.17, thus confirming the earlier work when these approximations are satisfied.
where the denominator is the total volume occupied by a group of N cells, and dSj is the surface of each volume element dvj. The idea is to make N small enough so that a good resolution is achieved (where the average is not smoothed unnecessarily), but large enough so that the function
If one applies the vector identity
The divergence (or Gauss's) theorem can be applied to the first term on the right-hand side of Equation 8.33, and since
Reference to Equation 8.7 identifies that
is a volume source (flow source) density.
8.6 SUMMARY OF THE SOURCE-FIELD MODELS
Table 8.1 gives the equations used in this chapter ( with equation numbers) for the different sources and their fields in an infinite homogeneous volume conductor.
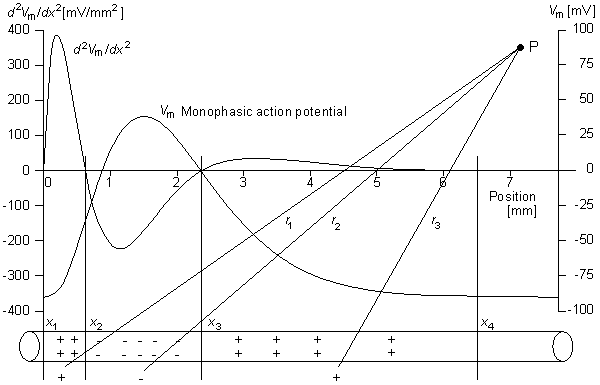
>0:x1 < x < x2

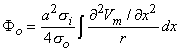
(08.21)  The reader will note that initially Fo was set equal to zero and now we have found a solution for Fo which, of course, is not zero. The underlying explanation of this apparent paradox is that Fo was ignored in deriving Equation 8.18 in comparison with Fi. Since the latter is perhaps 100 times larger, dropping Fo at that point should have negligible consequences. The interested reader can pursue the matter by introducing the value Fo found in Equation 8.21 into the rigorous version of Equation 8.18, namely
The reader will note that initially Fo was set equal to zero and now we have found a solution for Fo which, of course, is not zero. The underlying explanation of this apparent paradox is that Fo was ignored in deriving Equation 8.18 in comparison with Fi. Since the latter is perhaps 100 times larger, dropping Fo at that point should have negligible consequences. The interested reader can pursue the matter by introducing the value Fo found in Equation 8.21 into the rigorous version of Equation 8.18, namely

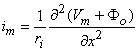
(08.18b)  Equation 8.21 may be integrated by parts. Since at the boundaries of the spatial activation, resting conditions are present,
Equation 8.21 may be integrated by parts. Since at the boundaries of the spatial activation, resting conditions are present,  Vm/
Vm/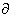 x = 0 and the integrated term drops out. Accordingly, we are left with
x = 0 and the integrated term drops out. Accordingly, we are left with

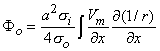
(08.22)

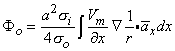
(08.23)  x = unit vector in the x-direction.
x = unit vector in the x-direction.
 Since both Equations 8.23 and 8.21 are mathematically the same, they necessarily evaluate the same field Fo. The physical interpretation of these expressions is that in Equation 8.21 the source is a (monopole) current density that lies on the axis, whereas in Equation 8.23 it is an axial dipole also lying along the axis. These are, of course, equivalent sources. Which source is prefeable to use depends on the shape of Vm(x); this will be illustrated in the following sections.
Since both Equations 8.23 and 8.21 are mathematically the same, they necessarily evaluate the same field Fo. The physical interpretation of these expressions is that in Equation 8.21 the source is a (monopole) current density that lies on the axis, whereas in Equation 8.23 it is an axial dipole also lying along the axis. These are, of course, equivalent sources. Which source is prefeable to use depends on the shape of Vm(x); this will be illustrated in the following sections.
 There are two approximations that underlie Equation 8.17 and that should be kept in mind. First, the configuration of the current element is approximated as a point source, but the current actually emerges from the membrane surface rather than a point (see Figure 8.2), and an axial segment could be characterized as a "ring source." For thin fibers this should be an acceptable simplification. Second, the field expression in Equation 8.17 is strictly for a point source in an unbounded space, whereas in reality the space is occluded by the fiber itself. This approximation is normally satisfactory. If, however, the extracellular space is itself limited, then the fiber probably cannot be ignored and the actual boundary value problem must be solved (Rosenfalck, 1969).
There are two approximations that underlie Equation 8.17 and that should be kept in mind. First, the configuration of the current element is approximated as a point source, but the current actually emerges from the membrane surface rather than a point (see Figure 8.2), and an axial segment could be characterized as a "ring source." For thin fibers this should be an acceptable simplification. Second, the field expression in Equation 8.17 is strictly for a point source in an unbounded space, whereas in reality the space is occluded by the fiber itself. This approximation is normally satisfactory. If, however, the extracellular space is itself limited, then the fiber probably cannot be ignored and the actual boundary value problem must be solved (Rosenfalck, 1969).
 The unbounded extracellular space is important to justify not only the use of the "free-space" point source field of Equation 8.7 but also the linear core-conductor expression of Equation 8.18, which is based on the assumption that ro
The unbounded extracellular space is important to justify not only the use of the "free-space" point source field of Equation 8.7 but also the linear core-conductor expression of Equation 8.18, which is based on the assumption that ro 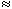 0 and Fi - Fo
0 and Fi - Fo 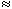 Vm. For the isolated fiber of "small" radius, Equations 8.21 and 8.23 appear to be well justified (Trayanova, Henriquez, and Plonsey, 1990).
Vm. For the isolated fiber of "small" radius, Equations 8.21 and 8.23 appear to be well justified (Trayanova, Henriquez, and Plonsey, 1990).

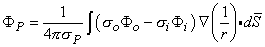
(08.28)
where F P = field at point P F i = potential just inside the membrane F o = potential just outside the membrane s i = conductivity inside the membrane s o = conductivity outside the membrane s P = conductivity at the field point
Source: Isolated cylindrical fiber
Conductor: Infinite, homogeneous
 If one applies Equation 8.28 to an isolated cylindrical fiber, then assuming only Fo
If one applies Equation 8.28 to an isolated cylindrical fiber, then assuming only Fo 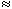 0 (hence Fi - Fo
0 (hence Fi - Fo 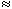 Vm ) leads to
Vm ) leads to

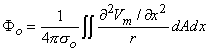
(08.29)

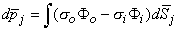
(08.30)  Since the heart contains around 5
Since the heart contains around 5  1010 cells of which perhaps 5% are active at any moment during depolarization, the number of dipole source elements is extremely high. Under these conditions one can define a volume dipole moment density function (i.e., a dipole moment per unit volume) by averaging the dipole elements in each small volume. That is,
1010 cells of which perhaps 5% are active at any moment during depolarization, the number of dipole source elements is extremely high. Under these conditions one can define a volume dipole moment density function (i.e., a dipole moment per unit volume) by averaging the dipole elements in each small volume. That is,

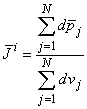
(08.31)  i is continuous from point to point (and does not reflect the underlying discrete cellular structure). Equation 8.31 is sometimes described as a coarse-grained average, since we do not let the volume, over which the average is taken, go to zero. The same considerations apply, for example, in electrostatics, where the charge density is normally considered to be a smooth, well-behaved function even though it reflects a discrete collection of finite point sources.
i is continuous from point to point (and does not reflect the underlying discrete cellular structure). Equation 8.31 is sometimes described as a coarse-grained average, since we do not let the volume, over which the average is taken, go to zero. The same considerations apply, for example, in electrostatics, where the charge density is normally considered to be a smooth, well-behaved function even though it reflects a discrete collection of finite point sources.
 The source function
The source function  i is a (volume) dipole density function. Consequently, the field it generates can be found by superposition, where
i is a (volume) dipole density function. Consequently, the field it generates can be found by superposition, where  idv is a single dipole to which Equation 8.12 applies. Thus, summing the field from all such elements, one obtains
idv is a single dipole to which Equation 8.12 applies. Thus, summing the field from all such elements, one obtains

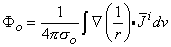
(08.32) 
 (
( i /r) =
i /r) =  (1/r)
(1/r)
 i + (1/r)
i + (1/r)

 i to Equation 8.32, then
i to Equation 8.32, then

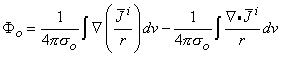
(08.33)  i = 0 at S (all source elements lie within the heart, and none are at the surface of integration), we get
i = 0 at S (all source elements lie within the heart, and none are at the surface of integration), we get

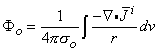
(08.34)

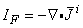
(08.35)  As was discussed in Section 7.2.2, one can interpret
As was discussed in Section 7.2.2, one can interpret  i as an impressed (i.e., an applied) current density. This current density is brought into being by the expenditure of chemical energy (i.e., the movement of ions due to concentration gradients); it is the primary cause for the establishment of an electric field. In contrast, we note that the current density,
i as an impressed (i.e., an applied) current density. This current density is brought into being by the expenditure of chemical energy (i.e., the movement of ions due to concentration gradients); it is the primary cause for the establishment of an electric field. In contrast, we note that the current density,  = s
= s , that is described by Ohm's law in Equation 8.4, is induced (i.e., it arises secondary to the presence of the aforementioned electric field
, that is described by Ohm's law in Equation 8.4, is induced (i.e., it arises secondary to the presence of the aforementioned electric field  ). Impressed currents
). Impressed currents  i are not established by the electric field
i are not established by the electric field  , since they originate in a source of energy, which is nonelectric in nature.
, since they originate in a source of energy, which is nonelectric in nature.
Table 8.1. Summary of the equations for different sources and their fields.
Source model
Source element
descriptionField Fo outside the source
Source density
Monopole
Io
(8.7)
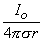
(8.7)
[point source]
Dipole
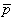 = Io
= Io
(8.9)
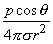
(8.15)
[point (dipole) source]
Single
isolated
fiber r » a
(where a =
fiber radius)im(x)dx
(8.16)
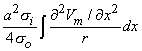
(8.21)
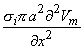
line
source
density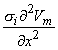
volume
source
density
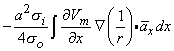
(8.23)
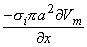
line
source
density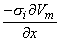
volume
source
density
Fiber bundle
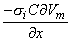
volume
source
density
C  0.4
0.4
Tripole
si
 2Vm/
2Vm/ x2
x2
>0:x2 < x < x3
>0:x3 < x < x4
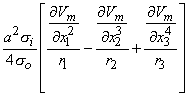
Vm refers here to a triangular
approximation of the actual
transmembrane potential
(exact form of the equation
in the text).(8.27)
Point sources on axis location: strength: x1 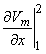
x1 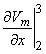
x1 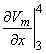
Single cell
(exact
formulation)(soFo - siFi)dS
(8.28)
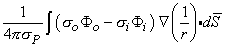
(8.28)
Double layer with
a strength of
(soFo - siFi) lying
in the cell membrane,
and oriented in the
outward direction
Isolated
cylindrical
fiber (exact
formulation)(soFo - siFi)dS
(8.28)
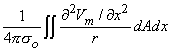
(8.29)
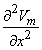
volume source
(flow source)
density
lying within
the fiber
Multicellular
tissue
(brain or
cardiac
tissue) idV
idV
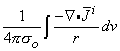
(8.34)
 i
ivolume dipole
density-
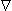

 i
ivolume source
(flow source)
density



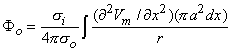
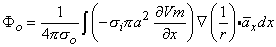
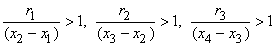
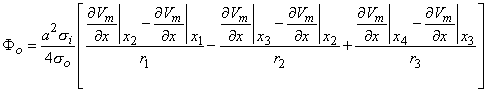
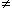 0) are assumed to be planar. All fibers in the bundle are assumed to be parallel and carrying similar action potentials; consequently, each fiber will contain a similar equivalent source density. This is shown as a dipole density and hence proportional to -
0) are assumed to be planar. All fibers in the bundle are assumed to be parallel and carrying similar action potentials; consequently, each fiber will contain a similar equivalent source density. This is shown as a dipole density and hence proportional to -
 in Equation 8.28 may be assumed to be constant in the integration over each cell. Thus each cell can be thought of as contributing a single lumped dipole source, which is simply the vector sum of its double layer surface elements. That is, the dipole for the jth cell, d
in Equation 8.28 may be assumed to be constant in the integration over each cell. Thus each cell can be thought of as contributing a single lumped dipole source, which is simply the vector sum of its double layer surface elements. That is, the dipole for the jth cell, d